Implementing a simple L-system parser
Here’s a very rough implementation of an L-system (Lindenmayer system) interpreter, parser and renderer, written in VB.NET
The current implementation is very basic and lacks many of the features available in more mature projects, such as LILiS.
Actually, the grammar to write l-system functions (or recipes) in LSysInt is very similar to that used by LILiS, with a few distinctions:
- A curve is defined using a name with its body enclosed between curly brackets.
- Parameters names must always end with a colon.
- So far, only a few parameters are supported:
- level: indicates the maximum recursion level
- axiom: indicates the initial conditions
- rule: indicates one or more rules to be applied to the axiom
- angle: defines the default angle when none is specified
- offsetX: defines a rendering origin offset in the horizontal direction
- offsetY: defines a rendering origin offset in the horizontal direction
- length: defines the default length of a segment when none is specified
- constant: defines a simple string-based substitution (no function support yet)
- Although LSysInt does not currently support “definitions”, most of the time these can be represented through one or more rules.
- These are the currently supported internal functions:
- F(x): move forward and draw x amount of pixels
- B(x): move backwards and draw x amount of pixels
- f(x): move forward x amount of pixels
- +(x): increase the angle by x amount
- -(x): decrease the angle by x amount
- [: save current vector state
- ]: restore saved vector state
- %(r, g, b, a): set vector color
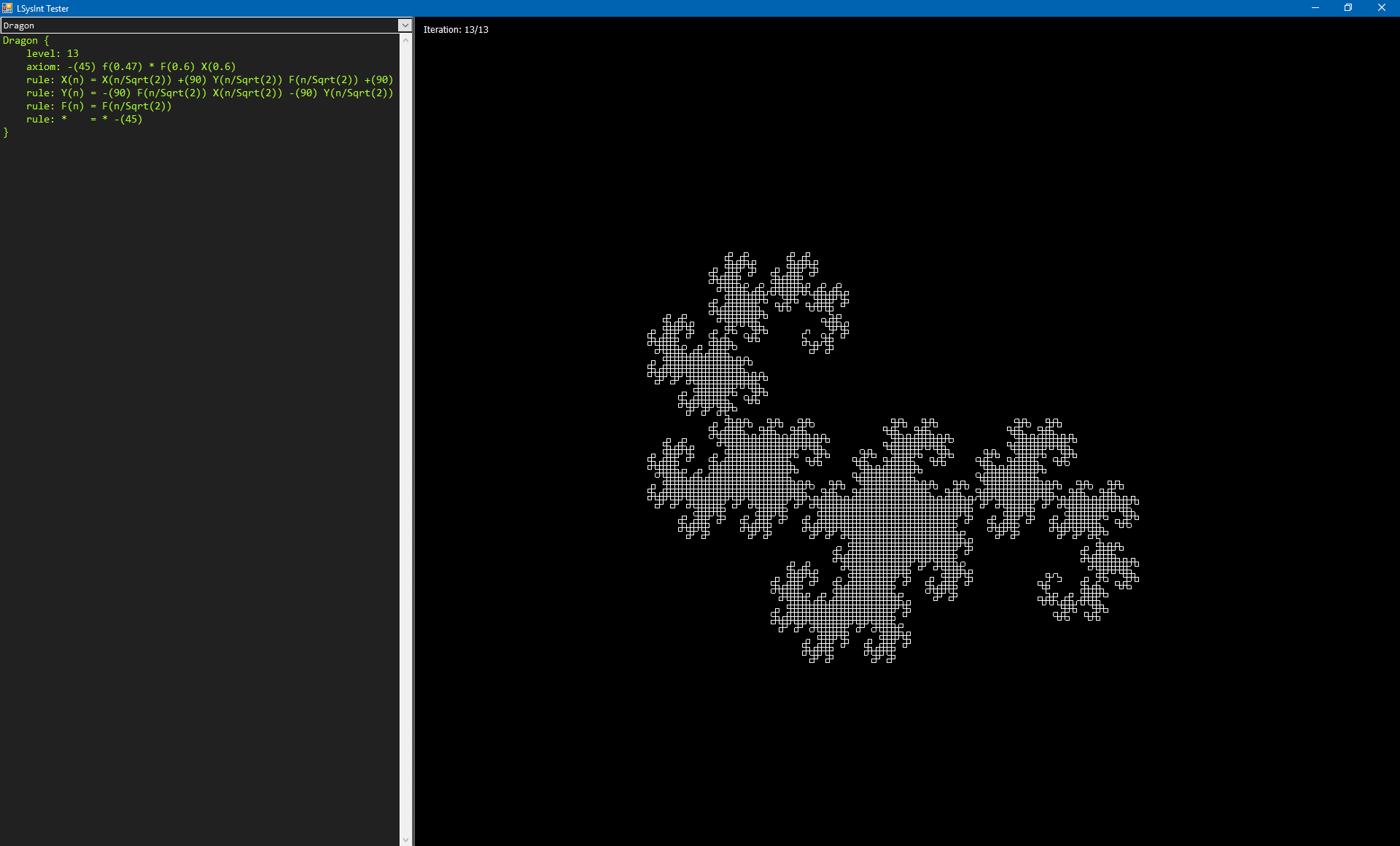
Here’s a sample code to render the dragon curve up to its 13th iteration:
Dragon {
level: 13
axiom: -(45) f(0.47) * F(0.6) X(0.6)
rule: X(n) = X(n/Sqrt(2)) +(90) Y(n/Sqrt(2)) F(n/Sqrt(2)) +(90)
rule: Y(n) = -(90) F(n/Sqrt(2)) X(n/Sqrt(2)) -(90) Y(n/Sqrt(2))
rule: F(n) = F(n/Sqrt(2))
rule: * = * -(45)
}
The source code is available at GitHub: https://github.com/morphx666/LSysInt
And the latest compiled version can be downloaded from the releases section at GitHub: https://github.com/morphx666/LSysInt/releases

Recent Comments