¿Por qué los tranques (cierres) en dominó tienen que dar par?
Esto es una explicación algo rebuscada de porqué la suma de las fichas restantes, luego de un traque (o cierre), en un juego de dominó, siempre debe dar par.
Si te aburre o molesta el exceso de matemáticas, salta a la conclusión para una explicación sencilla y directa al punto.
Axiomas:
- Hay 28 fichas en el dominó y 7 fichas con cada posible valor desde 0 hasta 6 por lo que
representa la suma de todos los valores de 0 a 6 para uno de los lados de las 7 fichas y
para el otro lado (lo que contempla los dobles). Sumando ambas fórmulas obtenemos que la suma de todas fichas es:
- Toda ficha presenta dos valores diferentes, exceptuando los dobles que presentan dos valores iguales.
- Debido a que la suma de todas las fichas es par, si la suma de fichas jugadas es par, también lo debe ser la suma de las fichas restantes.
- El tranque (o cierre) se realiza cuando se juegan todas las fichas de un número cuya suma, según el axioma 1, se da por la fórmula
, donde k es el valor de la ficha que cierra (tranca).
- Para fichas k pares
es impar y para fichas impares es par. Esto queda más explícito en esta versión de la fórmula:
Lo que confirma que la suma de un valor k impar produce un resultado par y, por el contrario, un valor de k par produce un resultado impar. - La suma de los valores adjuntos de dos fichas consecutivas siempre será par, ya que los números son iguales y 2k, para cualquier valor entero de k produce un número par. De tal forma se sabe que la concatenación de las fichas jugadas genera una suma par.
Según el axioma 6 y sabiendo que la suma de dos números iguales siempre será par, la concatenación de todas las fichas jugadas debe ser par, ya que en un tranque o cierre, existe una cantidad par de valores jugados.
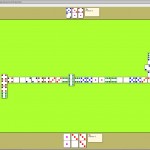
En el caso de la imagen (tomada de un juego en el xFX Domino), hay 2 unos, 6 dos, 4 tres, 6 cuatros, 4 cincos y, obviamente, 8 seis jugados.
Por lo tanto, la suma de fichas jugadas es:
Como se puede observar, todos los valores de las fichas están multiplicados por factores pares (2, 6, 4, 6, 4 y 8) lo que provocará que la suma total de las fichas jugadas sea par.
De tal forma y sabiendo que la suma total de fichas es par (ver axioma 1), al restar la suma de fichas jugadas deberá dar un resultado par:
Adendas:
- Debido a que la dominación con capicúa es una forma de tranque, también debe cumplir con esta regla.
- Dominar con doble, ya que la suma de los valores de todo doble es par, también debe cumplir con esta regla, siempre y cuando la otra cabeza sea par.
- Cuando no hay tranque se puede saber si el resultado será par o impar, tan solo comparando los valores de las dos cabezas.
Si una es impar y la otra no, el resultado deberá ser impar, si ambas son pares o impares, el resultado deberá ser par.

Recent Comments